티스토리 뷰
연결 리스트 - 두 개의 정렬된 리스트 합치기
단순 연결리스트(양방향 또는 원형 등이 아닌 단방향 연결리스트) l1과 l2에 숫자가 오름차순으로 저장되어있을 때, 리스트에 저장된 숫자의 오름차순을 그대로 유지하면서 두 단순 연결 리스트를 하나의 단순 연결리스트로 합친 단순 연결리스트를 반환하라.
문제를 풀기 앞서, 막연하게 생각하지 말고 하나의 예를 들어 어떻게 방향을 잡아야 할지 가늠해봅시다.

단순 연결리스트 l1의 길이는 m(=3), 단순 연결리스트 l2의 길이는 n(=4)라고 가정하겠습니다.
가장 먼저 떠오르는 방법!?
가장 먼저 떠오르는 방법은 단순 연결리스트 l1, l2를 합친 후, 정렬 알고리즘 중 하나를 사용하여 정렬된 단순 연결리스트를 얻는 방법일 것입니다.
두 단순 연결리스트 l1, l2를 합치면 다음과 같겠죠. (합치는 순서는 중요하지 않습니다. 어차피 정렬을 할 거니깐요)

그런 후 합쳐진 단순 연결리스트 l3를 정렬하면 다음과 같아집니다.

직관적이고 단순하며 구현도 비교적 간단할 거라고 생각이 됩니다.
하지만 이 방법의 시간 복잡도를 잠시 계산하여 보겠습니다.
두 단순 연결리스트를 합치는 연산은 O(m) 또는 O(n)
연결된 단순 연결리스트을 정렬하는 연산은 O((m+n)log(m+n)) 일 것입니다.
전체 연산의 시간 복잡도는 O((m+n)log(m+n)) 입니다.
두 단순 연결리스트를 합치는 작업이 O(1)이지 않냐라고 생각할 수 있지만, 두 연결 리스트는 단순 연결리스트이기 때문에 각 연결리스트의 마지막 노드(tail)에 대한 레퍼런스를 가지고 있지 않습니다. 합쳐질 단순 연결리스트의 앞에 올 단순 연결리스트의 마지막 노드까지 선형 탐색이 이루어져야 합니다.
더 최적화된 방법을!?
하지만, 애초에 각 단순 연결리스트는 정렬이 되어있는 상태인데, 또다시 정렬하는 것은 비효율적일 것 같고, 주어진 조건을 사용하지 않았다는 점에서 뭔가 더 최적화된 방법이 있지 않을까 고민해볼 수 있습니다.
사실 이러한 아이디어는 병합 정렬에서 한번 살펴보셨을 수 있습니다.
배열에서의 병합 정렬에서 정렬되어있는 두 배열을 합칠 때 사용하는 아이디어와 동일합니다. 하지만 그 경우는 인덱스를 사용하였다는 점과 현재는 노드의 레퍼런스를 사용하여야 한다는 점만 다를 뿐입니다.
각 단순 연결리스트의 시작노드부터 대소관계를 비교하여 실을 꿰듯이 각 단순 연결리스트의 노드들을 연결해나가는 것입니다. 그 과정을 살펴보도록 하겠습니다.

단순 연결리스트 l1의 시작 노드에 담긴 숫자 2와 단순 연결리스트 l2의 시작노드에 담긴 숫자 5를 비교합니다.

숫자 2가 숫자 5보다 작기 때문에 합쳐진 단순 연결 리스트에 숫자 2를 가진 노드를 연결하여 준 모습입니다.
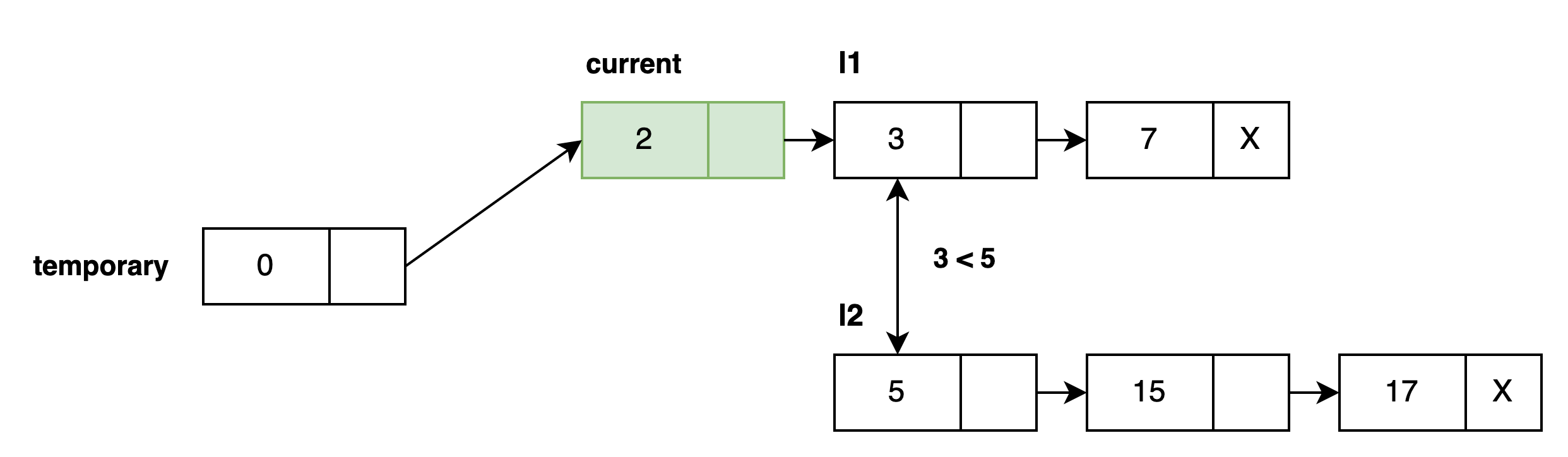
그런 후, 단순 연결리스트 l1의 시작 노드를 한 칸 뒤로 밀어줍니다 - 이전 노드는 연결이 되었으니 비교대상이 아니기 때문입니다 그런 후, 합친 단순 연결리스트에 연결한 노드(current)를 가리켜줍니다. - 최근에 연결한 노드의 정보를 가지고 있어야 그 뒤로 추가적인 연결이 가능하기 때문입니다.
그리고 숫자 2와 5를 비교했던 것처럼 동일한 작업을 반복하면 다음과 같아집니다.

여기서 주의하여할 점은 한쪽 단순 연결리스트가 먼저 끝이 날 수 있다는 점입니다. 그런 경우는 남은 단순 연결리스트의 노드들을 합친 단순 연결리스트의 끝에 이어주면 됩니다. 다음과 같이 말이죠.

그러면 이 방법은 처음 방법에 비해 얼마나 개선이 되었을지 시간 복잡도를 계산하여 보겠습니다. 최악의 경우 모든 노드에 대해서 대소 비교를 해야 하므로 두 단순 연결리스트의 길이의 합에 비례할 것입니다. 즉 O(m+n)입니다.
그럼 구현을!?
Java를 사용하여 위 방법을 구현해보도록 하겠습니다.
public class MergeTwoSortedLists {
private static class ListNode<T> {
private T data;
private ListNode<T> next;
public ListNode(T data, ListNode<T> next) {
this.data = data;
this.next = next;
}
}
private static ListNode<Integer> mergeTwoSortedLists(ListNode<Integer> l1, ListNode<Integer> l2) {
ListNode<Integer> temporary = new ListNode<>(0, null);
ListNode<Integer> current = temporary;
while (l1 != null && l2 != null) {
if (l1.data <= l2.data) {
current.next = l1;
l1 = l1.next;
} else {
current.next = l2;
l2 = l2.next;
}
current = current.next;
}
if (l1 != null) {
current.next = l1;
} else if (l2 != null) {
current.next = l2;
}
return temporary.next;
}
public static void main(String[] args) {
ListNode<Integer> l1 = new ListNode<>(2,
new ListNode<>(3, new ListNode<>(7, null))
);
ListNode<Integer> l2 = new ListNode<>(5,
new ListNode<>(11, new ListNode<>(15, null))
);
ListNode<Integer> l3 = mergeTwoSortedLists(l1, l2);
// l1 : 2 -> 3 -> 7 -> null
// l2 : 5 -> 11 -> 15 -> null
// l3 : 2 -> 3 -> 5 -> 7 -> 11 -> 15 -> null
while (l3 != null) {
System.out.print(l3.data + " -> ");
l3 = l3.next;
}
}
}
결과

마무리
사실상 단순 연결리스트를 직접 구현하여 사용하는 경우는 드문 게 사실입니다. 대부분은 추상화가 잘되어져 있어, 그 내부 구현을 모르더라도 사용하는데 큰 지장이 없기 때문이죠. 이러한 문제를 해결하면서 얻을 수 있는 점은 사고력이라고 생각합니다.
참고
Java에서 리스트 중 LinkedList는 양방향 연결리스트로 구현되어있습니다.
참고서적
- Total
- Today
- Yesterday
- 구현
- 쓰레드
- Java
- TDD
- dp
- 스트림
- Uber
- 회고
- 정렬
- kotlin
- 알고리즘
- 코딩인터뷰
- 해쉬
- 탐욕법
- 프로그래머스
- set
- dsu
- dfs
- JPA
- sql
- 코드 스니펫
- 우선순위큐
- 스택
- 비트연산
- 연결리스트
- 문자열
- k8s
- 오늘의집
- 카카오
- BFS
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
